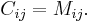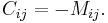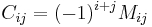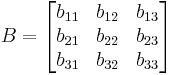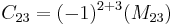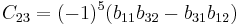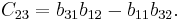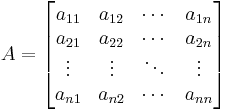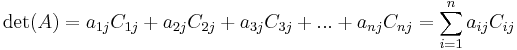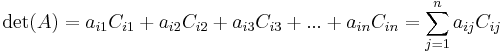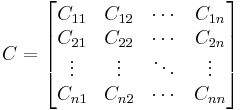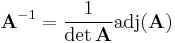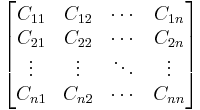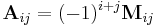Cofactor (linear algebra)
In linear algebra, the cofactor (sometimes called adjunct, see below) describes a particular construction that is useful for calculating both the determinant and inverse of square matrices. Specifically the cofactor of the (i, j) entry of a matrix, also known as the (i, j) cofactor of that matrix, is the signed minor of that entry.
Contents |
Informal approach to minors and cofactors
Finding the minors of a matrix A is a multi-step process:
- Choose an entry
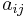 from the matrix.
from the matrix. - Cross out the entries that lie in the corresponding column
 and row
and row  .
. - Rewrite the matrix without the marked entries.
- Obtain the determinant
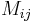 of this new matrix.
of this new matrix.
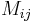 is termed the minor for entry
is termed the minor for entry 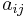 .
.
If i + j is an even number, the cofactor 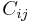 of
of 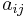 coincides with its minor:
coincides with its minor:
Otherwise, it is equal to the additive inverse of its minor:
Formal definition
If A is a square matrix, then the minor of its entry 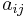 , also known as the i,j, or (i,j), or (i,j)th minor of A, is denoted by
, also known as the i,j, or (i,j), or (i,j)th minor of A, is denoted by 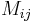 and is defined to be the determinant of the submatrix obtained by removing from A its i-th row and j-th column.
and is defined to be the determinant of the submatrix obtained by removing from A its i-th row and j-th column.
It follows:
and 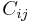 called the cofactor of
called the cofactor of 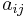 , also referred to as the i,j, (i,j) or (i,j)th cofactor of A.
, also referred to as the i,j, (i,j) or (i,j)th cofactor of A.
Example
Given the matrix
suppose we wish to find the cofactor C23. The minor M23 is the determinant of the above matrix with row 2 and column 3 removed.
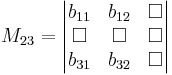 yields
yields 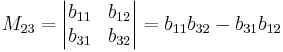
Using the given definition it follows that
Note: the vertical lines are an equivalent notation for det(matrix)
Cofactor expansion
Given the 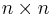 matrix
matrix
The determinant of A (denoted det(A)) can be written as the sum of the cofactors of any row or column of the matrix multiplied by the entries that generated them.
Cofactor expansion along the jth column:
Cofactor expansion along the ith row:
Matrix of cofactors
The matrix of cofactors for an 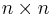 matrix A is the matrix whose (i,j) entry is the cofactor Cij of A. For instance, if A is
matrix A is the matrix whose (i,j) entry is the cofactor Cij of A. For instance, if A is
the cofactor matrix of A is
where Cij is the cofactor of aij.
Adjugate
The adjugate matrix is the transpose of the matrix of cofactors and is very useful due to its relation to the inverse of A.
The matrix of cofactors
when transposed becomes
A remark about different notations
In some books, including the so called "bible of matrix theory"[1] instead of cofactor the term adjunct is used. Moreover, it is denoted as Aij and defined in the same way as cofactor:
Using this notation the inverse matrix is written this way:
Keep in mind that adjunct is not adjugate or adjoint.
See also
References
- ^ Felix Gantmacher, Theory of matrices (1st ed., original language is Russian), Moscow: State Publishing House of technical and theoretical literature, 1953, p.491,
- Anton, Howard; Rorres, Chris (2005), Elementary Linear Algebra (9th ed.), John Wiley and Sons, ISBN 0-471-66959-8
External links
- MIT Linear Algebra Lecture on Cofactors at Google Video, from MIT OpenCourseWare
- PlanetMath